|
Guillaume Lauga I'm a postdoctoral researcher at Université Côte d'Azur with Samuel Vaiter. I defended my thesis in December 2024 at ENS Lyon, supervised by Paulo Gonçalves, Elisa Riccietti and Nelly Pustelnik. I was a member of the Inria OCKHAM team. During my PhD, I worked on multilevel optimization methods for proximal based algorithms, with applications to image restoration problems. Email / Tel: +33684021194 / CV (01/2026) / Scholar / Github |

|
ResearchI'm interested in optimization for imaging applications. Since the start of my PhD I investigate the convergence of proximal algorithms tailored for large-scale problems. |
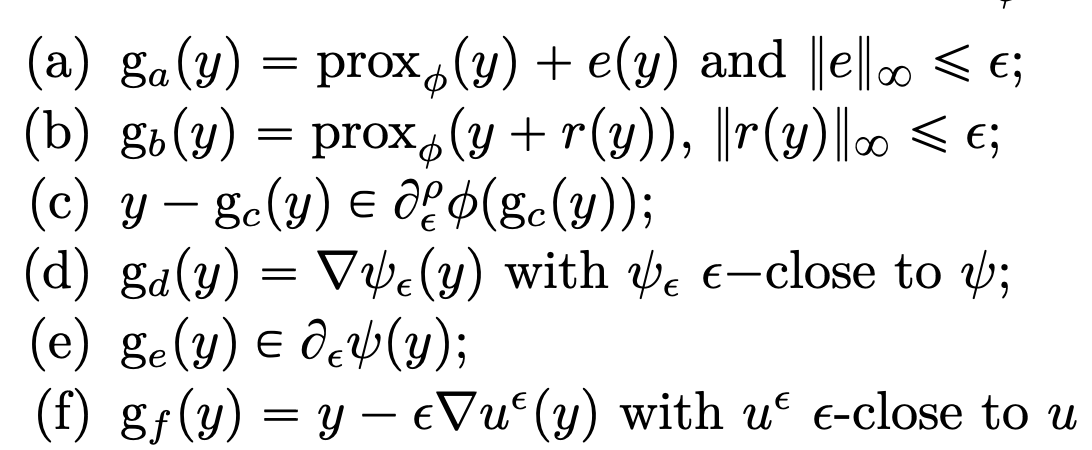
|
Characterizations of inexact proximal operators
Guillaume Lauga, Samuel Vaiter preprint, 2026 arXiv / HAL In the footsteps of Moreau and Gribonval et al, we propose some characterizations of inexact proximal operators to identify what is a good approximation of a proximal operator. We also investigate the convergence of inexact proximal algorithms in the presence of non-summable errors. |
|
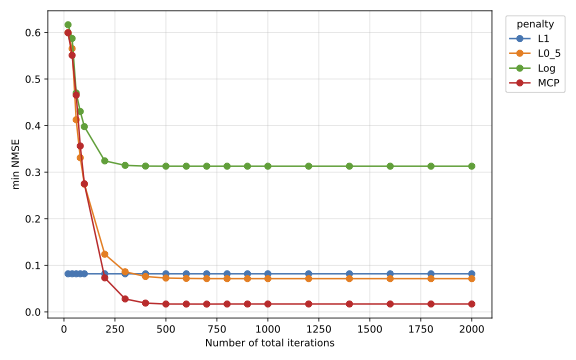
A block-coordinate descent framework for non-convex composite optimization. Application to sparse precision matrix estimation
Guillaume Lauga preprint, 2026 Code to reproduce the experiments / arXiv / HAL Reweighted optimization is a standard way to deal with non-convex penalties. We propose here a block-coordinate descent framework to tackle this kind of problems, removing the need of complete minimization between reweightings. This framework is applied to accelerate three variants of well known solvers of the non-convex Graphical Lasso problem: Graphical ISTA, QUIC and Primal GLasso. |
|
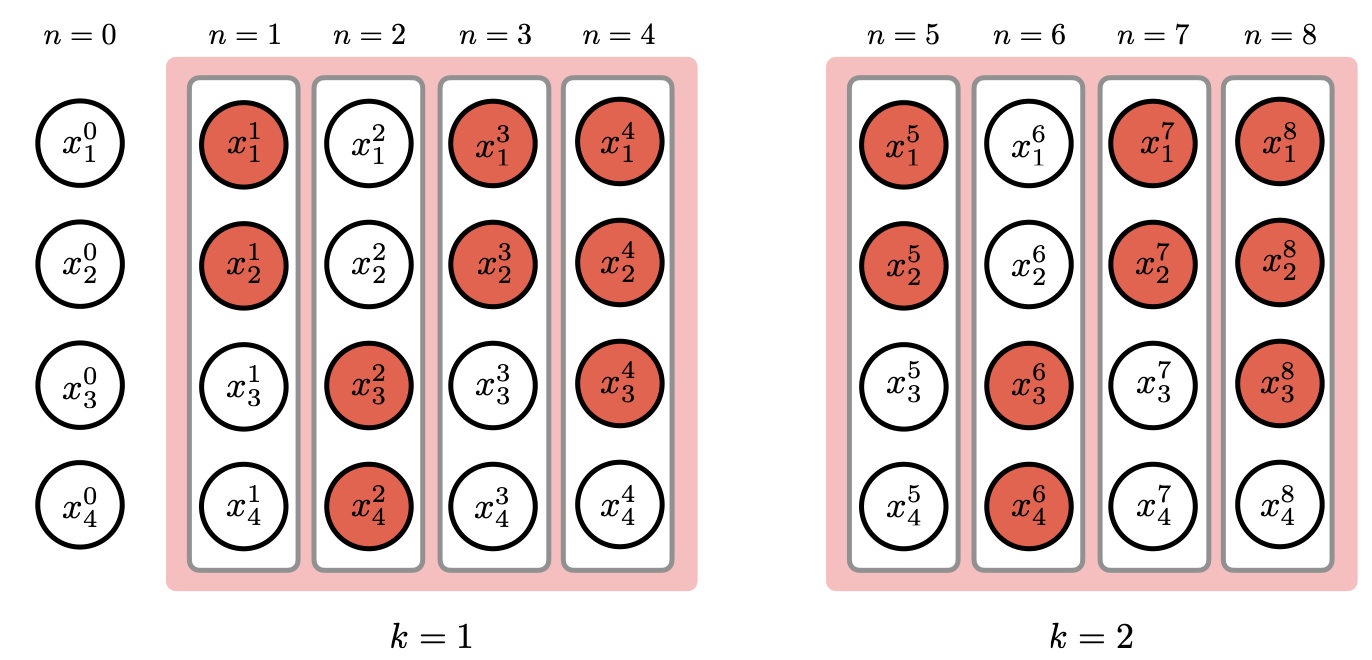
A flexible block-coordinate forward-backward algorithm for non-smooth and non-convex optimization.
Luis Briceño-Arias, Paulo Gonçalves, Guillaume Lauga, Nelly Pustelnik, Elisa Riccietti preprint, 2025 arXiv / HAL We propose a new deterministic BCD framework that allows for very flexible updates, while guaranteeing state-of-the-art convergence guarantees on non-smooth nonconvex optimization problems. While encompassing several update rules from the literature, this framework allows for priority on updates of particular blocks and correlations in the block selection between iterations, which is not permitted under the classical convergent stochastic framework. |
|
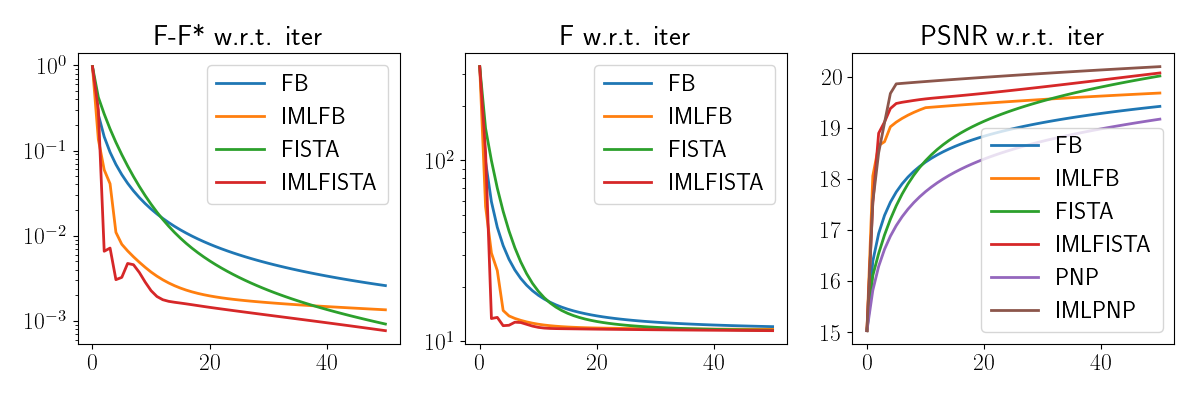
Python code for IML FISTA, compatible with DeepInverse
Repository containing a Python implementation of three multilevel algorithms: IML FB, IML FISTA and IML PNP to be compared to their single level counterparts. The code is compatible with the DeepInverse package, which allows to easily change the imaging application. 
|
|
|
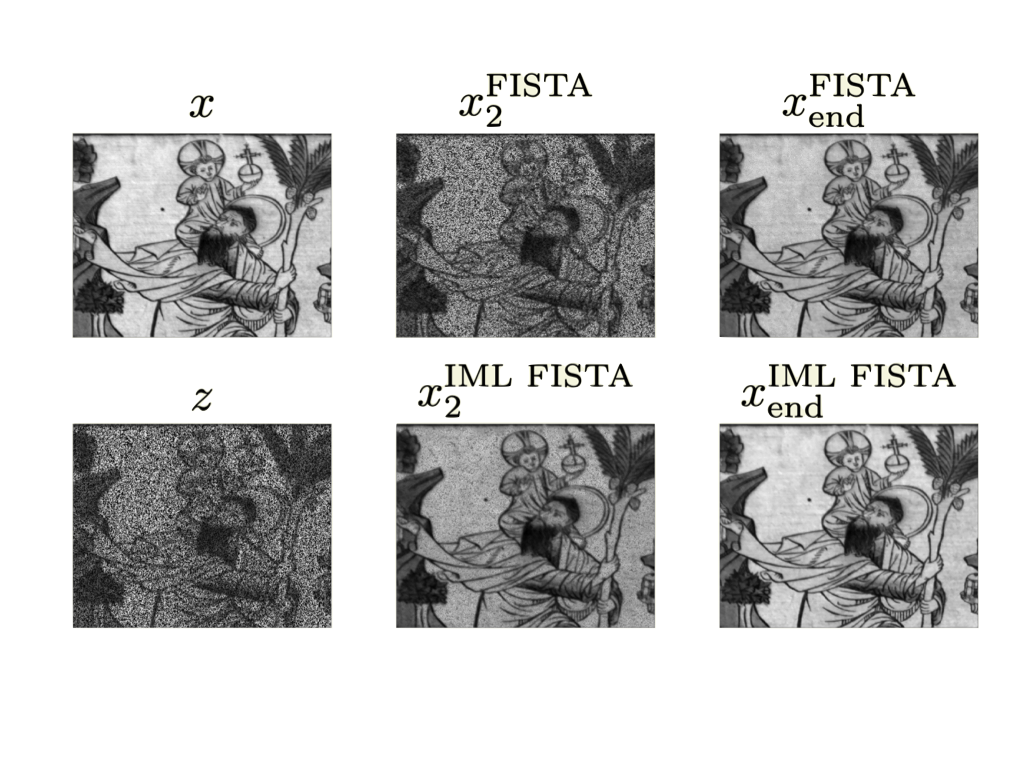
IML FISTA: A Multilevel Framework for Inexact and Inertial Forward-Backward. Application to Image Restoration
Guillaume Lauga, Elisa Riccietti, Nelly Pustelnik, Paulo Gonçalves SIAM Journal on Imaging Sciences, 2024 Matlab code / arXiv / HAL IML FISTA: An Inexact Multilevel FISTA. Optimal convergence guarantees on non-smooth convex optimization problems and ability to handle inexact computation of the proximity operator. Some applications to restoration of color and hyperspectral images. |
|
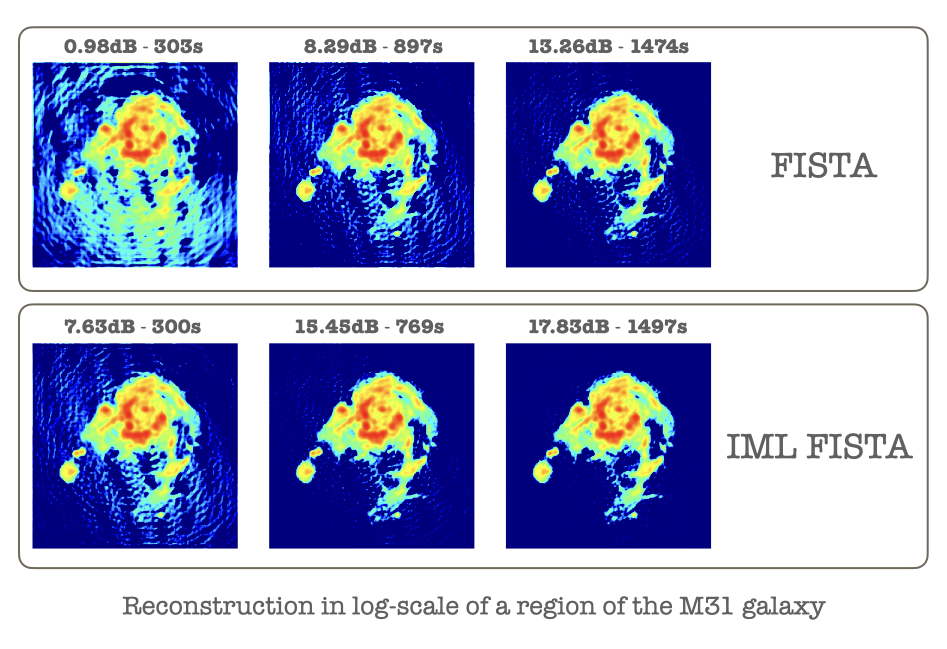
A multilevel framework for accelerating uSARA in radio-interferometric imaging
Guillaume Lauga, Audrey Repetti, Elisa Riccietti, Nelly Pustelnik, Paulo Gonçalves, Yves Wiaux EUSIPCO, 2024 (Poster) BASP Group project page / arXiv / HAL Application of IML FISTA to solve radio-interferometric imaging problems. Hierarchy of approximations built in the observation space rather than in the parameter space. |
|
Website source code from here. |

